Struktur Data Tree
Tree merupakan salah satu bentuk struktur data bukan linier yang menggambarkan bentuk hierarki antara elemen-elemen. Tree biasanya terdiri dari root (akar) dan node-node (simpul-simpul) yang berada di bawah root. Struktur seperti tree sangat banyak sekali dgunakan dalam dunia nyata, misalnya: struktur organisasi suatu perusahaan, pengaturan filesystem, daftar isi sebuah buku, dan masih banyak lagi.
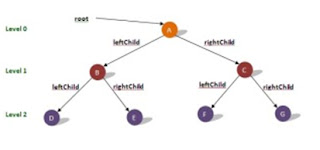
Ilustrasi struktur data tree:
Ilustrasi Tree
Degree (derajat) adalah jumlah edge yang keluar dan masuk dari sebuah node.
Contoh : node E memiliki in degree 1 dan out degree 2
Root (akar) adalah node yang memiliki derajat keluar >=0 dan derajat masuk = 0.
Contoh : node A adalah root
Subtree / child adalah bagian salah satu node dibawah root sampai ke bawah.
Contoh : tree C adalah right subtree dari A dan tree B merupakan left subtree dari A
node G dan F merupakan child dari node C
node F merupakan parent dari node J dan K
Ancestor adalah Node yang berada di atas node lain.
Contoh : node B adalah ancestor dari node E
Descendant adalah node yang berada di bawah node lain.
Contoh : node E adalah descendant dari node A.
Leaf (daun) adalah semua node yang derajat masuknya 1 dan derajat keluarnya 0.
Contoh : node D, H, I, J, K, dan G adalah leaf
Sibling adalah node yang mempunyai level yang sama dan parent yang sama.
Contoh : node D adalah sibling dari node A
Height (ketinggian) adalah level tertinggi dari tree ditambah 1.
Contoh : height dari tree A adalah 3 + 1 = 4
Weight (bobot) adalah jumlah leaf(daun) pada tree.
Contoh : weight dari tree A adalah 6
Contoh : node E memiliki in degree 1 dan out degree 2
Root (akar) adalah node yang memiliki derajat keluar >=0 dan derajat masuk = 0.
Contoh : node A adalah root
Subtree / child adalah bagian salah satu node dibawah root sampai ke bawah.
Contoh : tree C adalah right subtree dari A dan tree B merupakan left subtree dari A
node G dan F merupakan child dari node C
node F merupakan parent dari node J dan K
Ancestor adalah Node yang berada di atas node lain.
Contoh : node B adalah ancestor dari node E
Descendant adalah node yang berada di bawah node lain.
Contoh : node E adalah descendant dari node A.
Leaf (daun) adalah semua node yang derajat masuknya 1 dan derajat keluarnya 0.
Contoh : node D, H, I, J, K, dan G adalah leaf
Sibling adalah node yang mempunyai level yang sama dan parent yang sama.
Contoh : node D adalah sibling dari node A
Height (ketinggian) adalah level tertinggi dari tree ditambah 1.
Contoh : height dari tree A adalah 3 + 1 = 4
Weight (bobot) adalah jumlah leaf(daun) pada tree.
Contoh : weight dari tree A adalah 6
BINARY TREE
Sebuah tree dengan syarat bahwa tiap node hanya boleh memiliki maksimal 2 subtree yang disebut sebagai subpohon kiri(left subtree) dan subpohon kanan (right subtree) dan kedua subtree tersebut harus terpisah, atau dengan kata lain tiap node dalam binary tree hanya boleh memiliki paling banyak 2 child.
Sebuah tree dengan syarat bahwa tiap node hanya boleh memiliki maksimal 2 subtree yang disebut sebagai subpohon kiri(left subtree) dan subpohon kanan (right subtree) dan kedua subtree tersebut harus terpisah, atau dengan kata lain tiap node dalam binary tree hanya boleh memiliki paling banyak 2 child.
Binary tree terdiri dari :
- Full Binary Tree : semua node (kecuali leaf pasti memiliki 2 anak dan tiap subtree memiliki panjang path yang sama)
Full Binary Tree
- Complete Binary Tree : mirip dengan full binary tree, tetapi tiap subtree boleh memiliki panjang path yang berbeda dan tiap node (kecuali leaf memiliki 2 anak)
Complete Binary Tree
- Skewed Binary Tree : binary tree yang semua nodenya (kecuali leaf) hanya memiliki satu anak
Skewed Binary Tree
BINARY SEARCH TREE
Binary tree dengan sifat bahwa nilai dari semua left child harus lebih kecil daripada nilai dari right child dan parentnya.
Contoh :
Binary tree dengan sifat bahwa nilai dari semua left child harus lebih kecil daripada nilai dari right child dan parentnya.
Contoh :
Binary Search Tree
Contoh Implementasi Binary Search Tree :
/**
* Program membuat binary tree yang memiliki 2 anak dimana insertion
* dilakukan secara terurut, dimana data yang lebih kecil diletakkan di kiri
* dan yang lebih besar diletakkan di kanan.
* @author : Jeffrey Hermanto Halimsetiawan
* Selasa, 1 April 2008
**/
import java.util.*;
class Node{
int data;
Node left;
Node right;
Node(int x){
this.data = x;
}
}
public class BinTree{
private Node root;
/**
* Mengecek apakah tree masih kosong
**/
private boolean isEmpty(){
return (root == null);
}
/**
* Memasukkan suatu nilai ke dalam tree.
* Jika nilai tersebut lebih kecil dari nilai node, maka bergerak ke kiri terus
* hingga menjadi child, begitu juga sebaliknya.
**/
public void insert(int input){
Node temp = new Node(input);
if (isEmpty())
root = temp;
else {
Node cursor = root,
parent = null;
while (cursor != null){
parent = cursor;
if (input < cursor.data)
cursor = cursor.left;
else
cursor = cursor.right;
}
/**
* Menambahkan Node baru pada kiri/kanan Node parent bergantung
* pada nilai input dan nilai yang disimpan Node parent
**/
if (input < parent.data){
parent.left = temp;
return;
}
else {
parent.right = temp;
return;
}
}
}
/**
* Mencari suatu nilai dalam tree berdasarkan prinsip :
* Selama belum menemukan nilai yang sama,
* Jika nilai yang dicari lebih kecil dari nilai yang disimpan dalam Node
* maka bergerak ke left Child begitu juga sebaliknya.
**/
public Node find(int key){
Node cursor = root;
while (cursor != null){
if (cursor.data == key)
return cursor;
else if (key < cursor.data)
cursor = cursor.left;
else
cursor = cursor.right;
}
return null;
}
public boolean delete(int key){
Node cursor = root,
parent = null;
boolean found = false,
isLeftChild = true; //menandai apakah Node yang dihapus merupakan left child
if (!isEmpty()){
while (cursor != null){
parent = cursor;
if (key == cursor.data){
found = true;
break;
}
else if (key < cursor.data){
isLeftChild = true;
cursor = cursor.left;
}
else {
isLeftChild = false;
cursor = cursor.right;
}
}
if (!found)
return false;
else {
/**
* Untuk menghapus leaf (tidak punya child)
**/
if (cursor.left == null && cursor.right == null){
if (cursor == root)
root = null;
else if (isLeftChild)
parent.left = null;
else
parent.right = null;
}
/**
* Jika node yang akan dihapus hanya memiliki salah satu subtree
* maka tinggal memindahkan subtree menggantikan node yang dihapus
**/
else if (cursor.left == null){
if (cursor == root)
root = cursor.right;
else if (isLeftChild)
parent.left = cursor.right;
else
parent.right = cursor.right;
}
else if (cursor.right == null){
if (cursor == root)
root = cursor.left;
else if (isLeftChild)
parent.left = cursor.left;
else
parent.right = cursor.left;
}
/**
* Jika node yang akan dihapus memiliki 2 child, maka cari successornya
* dengan fungsi getSuccessor kemudian hubungkan subtree bagian kanan
* dari node yang dihapus dengan successor
**/
else {
Node successor = getSuccessor(cursor);
if (cursor == root)
root = successor;
else if (isLeftChild)
parent.left = successor;
else
parent.right = successor;
//menyambung successor dengan cursor.right
successor.right = cursor.right;
}
}
}
return true;
}
/**
* Mencari nilai terbesar yang mendekati nilai yang disimpan Node
* yang dihapus, Ilustrasi :
*
* 65
* 59 72
* 32 64
* 62
* misal : nilai yang dihapus 65, maka nilai terbesar yang mendekati adalah 64.
* maka ambil 64 sebagai successor, kemudian gabungkan
* 59
* 32 63
* Kemudian satukan keduanya :
* 64
* 59
* 32 63
* Jadilah urutan tree yang masih memenuhi syarat Binary Search Tree
**/
private Node getSuccessor(Node localNode){
Node parent = null,
successor = localNode,
cursor = localNode.left;
while (cursor != null){
parent = successor;
successor = cursor;
cursor = cursor.right;
}
if (successor != localNode.left){
parent.right = successor.left;
successor.left = localNode.left;
}
return successor;
}
/**
* Method traverse untuk mengelilingi Node-Node dalam tree
**/
public void traverse(int tipe){
switch (tipe){
case 1:
System.out.print("\nPreorder traversal:\n");
preOrder(root);
break;
case 2:
System.out.print("\nInorder traversal:\n");
inOrder(root);
break;
case 3:
System.out.print("\nPostorder traversal:\n");
postOrder(root);
break;
}
System.out.println('\n');
}
private void preOrder(Node localRoot){
if (localRoot == null) return;
System.out.print(localRoot.data+" ");
preOrder(localRoot.left);
preOrder(localRoot.right);
}
private void inOrder(Node localRoot){
if (localRoot == null) return;
inOrder(localRoot.left);
System.out.print(localRoot.data+" ");
inOrder(localRoot.right);
}
private void postOrder(Node localRoot){
if (localRoot == null) return;
postOrder(localRoot.left);
postOrder(localRoot.right);
System.out.print(localRoot.data+" ");}
AVL TREE
Dalam ilmu komputer , sebuah pohon AVL adalah sebuah pohon pencarian biner menyeimbangkan diri , dan itu seperti pertama struktur data yang ditemukan. [1] Dalam sebuah pohon AVL, dengan ketinggian dari dua anak sub pohon dari simpul apapun berbeda dengan paling banyak satu. Pencarian, penyisipan, dan penghapusan semua mengambil O (log n) baik di rata-rata dan kasus-kasus terburuk, dimana n adalah jumlah node dalam pohon sebelum operasi. Pemasangan dan penghapusan mungkin memerlukan pohon yang akan rebalanced oleh satu atau lebih rotasi pohon .
Pohon AVL ini dinamai setelah dua penemu soviet, GM Adelson-Velskii dan EM Landis , yang diterbitkan di koran mereka 1962 "Sebuah algoritma untuk organisasi informasi." [2]
Faktor keseimbangan dari sebuah node adalah tinggi subpohon kiri minus tinggi subpohon kanan (kadang-kadang berlawanan) dan node dengan 1 keseimbangan, faktor 0, atau -1 dianggap seimbang. Sebuah node dengan saldo faktor lain dianggap tidak seimbang dan membutuhkan rebalancing pohon. Faktor keseimbangan adalah baik disimpan langsung pada setiap node atau dihitung dari ketinggian dari subpohon.
pohon AVL yang sering dibandingkan dengan pohon merah-hitam karena mereka mendukung set yang sama operasi dan karena pohon merah-hitam juga mengambil O (log n) waktu untuk operasi dasar. Pohon AVL berperforma lebih baik dibandingkan-hitam pohon-intensif merah untuk aplikasi pencarian. [3] Pohon AVL algoritma menyeimbangkan muncul dalam kurikulum ilmu komputer banyak.
| Contents Isi [hide] |
[ sunting ] Operasi
Operasi dasar dari sebuah pohon AVL melibatkan melakukan tindakan yang sama seperti yang akan dilakukan pada seimbang pohon pencarian biner , namun modifikasi didahului atau diikuti oleh satu atau lebih operasi disebut rotasi pohon , yang membantu untuk mengembalikan keseimbangan ketinggian subpohon .
[ sunting ] Pencarian
Lookup dalam sebuah pohon AVL dilakukan persis seperti dalam sebuah pohon pencarian biner tidak seimbang. Karena tinggi-balancing dari pohon, lookup mengambil O (log n) waktu. Tidak ada tindakan khusus yang perlu diambil, dan struktur pohon tidak dimodifikasi oleh pencarian. (Hal ini berbeda untuk melebarkan pohon lookup, yang melakukan memodifikasi Teman-pohon struktur mereka.)
Jika setiap node tambahan catatan ukuran subpohon (termasuk dirinya sendiri dan keturunannya), maka node dapat diambil dengan indeks dalam O (log n) juga.
Setelah node telah ditemukan di sebuah pohon seimbang, atau sebelumnya node berikutnya dapat dieksplorasi dalam diamortisasi waktu yang konstan. Beberapa kasus memerlukan melintasi sampai 2 × log (n) link. Namun menjelajahi semua node n di pohon dengan cara ini akan menggunakan setiap link tepat dua kali, dan ada link n -1, sehingga biaya diamortisasi adalah 2 × (n -1) / n, sekitar 2.
[ sunting ] Penyisipan
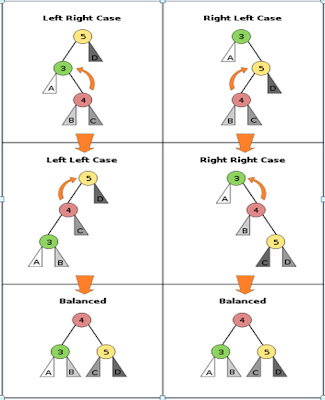
Bergambar keterangan tentang bagaimana rotasi menyebabkan rebalancing pohon, dan kemudian menapak langkah seseorang menuju akar memperbarui faktor keseimbangan node.
Setelah memasukkan sebuah node, perlu untuk memeriksa setiap nenek moyang node untuk konsisten dengan aturan AVL. Untuk setiap node diperiksa, jika faktor keseimbangan tetap -1, 0, atau +1 maka tidak ada rotasi diperlukan. Namun, jika faktor saldo menjadi ± 2 maka subtree berakar pada node ini tidak seimbang. Jika insersi dilakukan secara serial, masing-masing setelah insersi, paling banyak dua rotasi pohon diperlukan untuk mengembalikan seluruh pohon aturan AVL.
Ada empat kasus yang perlu dipertimbangkan, dimana dua diantaranya simetris dengan dua lainnya. Misalkan R anak kanan dari P. Biarkan L adalah anak kiri dari P.
Kanan-Kanan-Kiri kasus dan kasus Kanan: Jika faktor keseimbangan P adalah -2, maka subtree kanan melampaui subtree kiri dari node yang diberikan, dan faktor saldo anak kanan (R) harus diperiksa. If the balance factor of R is ≤ 0, a left rotation is needed with P as the root. Jika faktor keseimbangan R ≤ 0, sebuah rotasi kiri diperlukan dengan P sebagai root. Jika faktor keseimbangan R +1, sebuah rotasi kiri ganda (berkenaan dengan P) diperlukan. The first rotation is a right rotation with R as the root. Rotasi rotasi pertama adalah benar dengan R sebagai root. Yang kedua adalah rotasi kiri dengan P sebagai root.
Waktu-Waktu kasus dan kasus-Kanan Waktu: Jika faktor keseimbangan P +2, maka subtree kiri melampaui subtree kanan dari node yang diberikan, dan faktor keseimbangan anak kiri (L) harus diperiksa. Jika faktor keseimbangan L ≥ 0, sebuah rotasi yang tepat diperlukan dengan P sebagai root. Jika faktor keseimbangan L adalah -1, rotasi kanan dua kali (berkenaan dengan P) diperlukan. The second is a right rotation with P as the root. Yang kedua adalah rotasi benar dengan P sebagai root.
Algoritma untuk semua di atas empat kasus dapat ditemukan di sini .
[ sunting ] Penghapusan
Jika node adalah daun atau hanya memiliki satu anak, menghapusnya. Jika tidak, ganti dengan baik terbesar di subpohon kiri (pendahulunya inorder) atau terkecil di subpohon kanan (pengganti inorder), dan menghapus simpul tersebut. Node yang ditemukan sebagai pengganti memiliki paling banyak satu subpohon. Setelah penghapusan, menelusuri jalan kembali pohon (induk pengganti) untuk akar, menyesuaikan faktor saldo sesuai kebutuhan.
Seperti dengan semua pohon biner, di-order pengganti node adalah anak kiri-sebagian besar subpohon kanan, dan dalam node-order pendahulunya adalah anak paling kanan dari subpohon kirinya. Dalam kedua kasus, node ini akan memiliki nol atau satu anak-anak. Hapus itu menurut salah satu dari dua kasus sederhana di atas.
Selain menyeimbangkan dijelaskan di atas untuk insert, jika faktor keseimbangan untuk pohon adalah 2 dan bahwa dari subpohon kiri adalah 0, sebuah rotasi yang tepat harus dilakukan pada P. Cermin kasus ini juga diperlukan. menapak bisa berhenti jika faktor saldo menjadi -1 atau +1 menunjukkan bahwa tinggi subtree yang tetap tidak berubah. If the balance factor becomes 0 then the height of the subtree has decreased by one and the retracing needs to continue. Jika faktor keseimbangan menjadi 0 maka ketinggian subtree mengalami penurunan oleh satu dan menapak kebutuhan untuk melanjutkan. Jika faktor keseimbangan menjadi -2 atau +2 maka subtree tidak seimbang dan perlu diputar untuk memperbaikinya. Jika rotasi daun faktor keseimbangan subtree di 0 menapak kemudian menuju root harus terus sejak ketinggian subpohon ini mengalami penurunan sebesar satu. Hal ini berbeda untuk sebuah penyisipan di mana sebuah rotasi yang mengakibatkan faktor keseimbangan 0 menunjukkan bahwa ketinggian subtree telah tetap tidak berubah.
Waktu yang dibutuhkan adalah O (log n) untuk pencarian, ditambah maksimum O (log n) rotasi dalam perjalanan kembali ke akar, sehingga operasi dapat diselesaikan dalam O (log n) waktu.
[ sunting ] Perbandingan dengan struktur lain
Kedua pohon AVL dan pohon merah-hitam yang self-balancing pohon pencarian biner, sehingga mereka sangat mirip matematis. Operasi untuk menyeimbangkan pohon berbeda, tetapi keduanya terjadi dalam waktu yang konstan. Perbedaan yang nyata antara keduanya adalah ketinggian membatasi. Untuk pohon n ukuran:
- Tinggi pohon AVL's An benar-benar kurang dari: [4]
- Merah hitam pohon-tinggi adalah paling lama 2 2log (n + 1) [5]
Pohon AVL lebih kaku seimbang dari pohon-Hitam Merah , yang menyebabkan lebih lambat penyisipan dan penghapusan tetapi pengambilan lebih cepat.